KNN의 문제점
import numpy as np
perch_length = np.array(
[8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0,
21.0, 21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5,
22.5, 22.7, 23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5,
27.3, 27.5, 27.5, 27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0,
36.5, 36.0, 37.0, 37.0, 39.0, 39.0, 39.0, 40.0, 40.0, 40.0,
40.0, 42.0, 43.0, 43.0, 43.5, 44.0]
)
perch_weight = np.array(
[5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0,
110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0,
130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0,
197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0,
514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0,
820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0,
1000.0, 1000.0]
)KNN의 한계를 해결한, 선형 회귀에 대해 알아보겠습니다.
http://bit.ly/perch_data 에서 불러온 데이터입니다.
from sklearn.model_selection import train_test_split
# 훈련 세트와 테스트 세트로 나눕니다
train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight, random_state=42)
# 훈련 세트와 테스트 세트를 2차원 배열로 바꿉니다
train_input = train_input.reshape(-1, 1)
test_input = test_input.reshape(-1, 1)저번 글에서도 나온 train_test_split 입니다.
기계학습에서 매우 많이 나오므로 꼭 알아두셔야 하는 부분입니다. train과 test의 순서도 헷갈리면 안됩니다!
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor(n_neighbors=3)
# k-최근접 이웃 회귀 모델을 훈련합니다
knr.fit(train_input, train_target)train_input, train_target으로 모델을 훈련해줍니다.
import matplotlib.pyplot as plt
# 50cm 농어의 이웃을 구합니다
distances, indexes = knr.kneighbors([[50]])
# 훈련 세트의 산점도를 그립니다
#x 축 = 길이
#y 축 = 무게
plt.scatter(train_input, train_target)
# 훈련 세트 중에서 이웃 샘플만 다시 그립니다.
plt.scatter(train_input[indexes], train_target[indexes], marker='D')
# 50cm 농어 데이터
plt.scatter(50, 1033, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()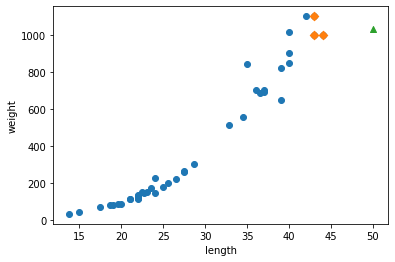
원으로 표시된 것은 존재하는 데이터, 마름모로 되어 있는 것은 삼각형이 이웃하게 되는 데이터, 삼각형은 새로 추가할 데이터입니다.
보시다시피 삼각형 데이터는 멀리 떨어져 있어서 이웃한 데이터를 찾기 곤란한 상황에 놓이게 되고, 이럴 상황이 지속될 경우 그래프가 일정 구간에서 직선이 되는 현상이 발생합니다.
# 100cm 농어의 이웃을 구합니다
distances, indexes = knr.kneighbors([[100]])
# 훈련 세트의 산점도를 그립니다
plt.scatter(train_input, train_target)
# 훈련 세트 중에서 이웃 샘플만 다시 그립니다
plt.scatter(train_input[indexes], train_target[indexes], marker='D')
# 100cm 농어 데이터
plt.scatter(100, 1033, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()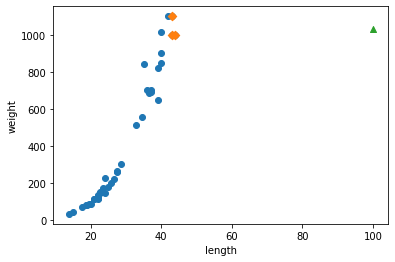
극단적으로 간다면, 이런 상황에 놓이게 됩니다.
문제점 해결, 선형 회귀
from sklearn.linear_model import LinearRegression선형 회귀는 영어로 Linear Regression이라 합니다.
lr = LinearRegression()
# 선형 회귀 모델 훈련
lr.fit(train_input, train_target)선형 회귀에 train_input, train_target 데이터를 학습시킵니다.
# 훈련 세트의 산점도를 그립니다
plt.scatter(train_input, train_target)
# 15에서 50까지 1차 방정식 그래프를 그립니다
plt.plot([15, 50], [15*lr.coef_+lr.intercept_, 50*lr.coef_+lr.intercept_])
# 50cm 농어 데이터
plt.scatter(50, 1241.8, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()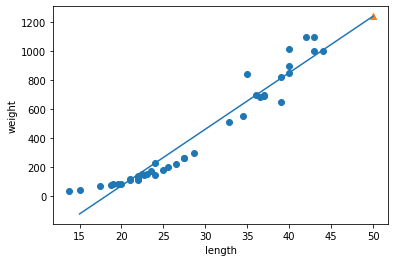
전보다 깔끔한 그래프가 그려졌습니다.
하지만 뭔가 아쉽습니다, 그래프가 데이터에 딱 맞게 곡선으로 되어 있다면 어떨까요?
예쁘게 곡선으로, 다항 회귀
# np.column_stack
train_poly = np.column_stack((train_input ** 2, train_input))
test_poly = np.column_stack((test_input ** 2, test_input))데이터를 제곱하여서 이차방정식을 만들 준비를 합니다.
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.predict([[50**2, 50]]))
# [1573.98423528]아까와 동일한 방식으로 학습하여 줍니다.
#기울기와 절편
print(lr.coef_, lr.intercept_)
# [ 1.01433211 -21.55792498] 116.05021078278264이차함수이므로 기울기와 절편이 존재합니다. 한번 확인해 봅시다.
# 구간별 직선을 그리기 위해 15에서 49까지 정수 배열을 만듭니다
point = np.arange(15, 50)
# 훈련 세트의 산점도를 그립니다
plt.scatter(train_input, train_target)
# 15에서 49까지 2차 방정식 그래프를 그립니다
plt.plot(point, 1.01*point**2 - 21.6*point + 116.05)
# 50cm 농어 데이터
plt.scatter([50], [1574], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()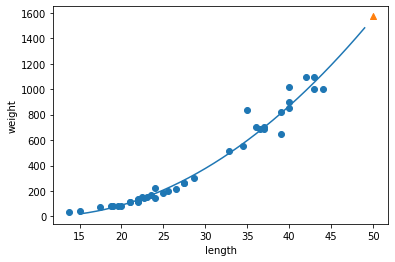
짠, 이렇게 예쁜 그래프가 완성되었습니다.
'🧠 인공지능' 카테고리의 다른 글
| 패턴 인식, 자료 분석 - SVM (0) | 2022.10.24 |
|---|---|
| FinanceDataReader로 주식 예측하기 (0) | 2022.09.21 |
| 경사하강법을 통해 오차 줄이기 (0) | 2022.09.19 |
| 기계학습에도 트리 구조가 있다? 의사 결정 트리 (0) | 2022.09.19 |
| Naive Bayes과 Iris (0) | 2022.09.04 |
KNN의 문제점
import numpy as np
perch_length = np.array(
[8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0,
21.0, 21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5,
22.5, 22.7, 23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5,
27.3, 27.5, 27.5, 27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0,
36.5, 36.0, 37.0, 37.0, 39.0, 39.0, 39.0, 40.0, 40.0, 40.0,
40.0, 42.0, 43.0, 43.0, 43.5, 44.0]
)
perch_weight = np.array(
[5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0,
110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0,
130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0,
197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0,
514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0,
820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0,
1000.0, 1000.0]
)KNN의 한계를 해결한, 선형 회귀에 대해 알아보겠습니다.
http://bit.ly/perch_data 에서 불러온 데이터입니다.
from sklearn.model_selection import train_test_split
# 훈련 세트와 테스트 세트로 나눕니다
train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight, random_state=42)
# 훈련 세트와 테스트 세트를 2차원 배열로 바꿉니다
train_input = train_input.reshape(-1, 1)
test_input = test_input.reshape(-1, 1)저번 글에서도 나온 train_test_split 입니다.
기계학습에서 매우 많이 나오므로 꼭 알아두셔야 하는 부분입니다. train과 test의 순서도 헷갈리면 안됩니다!
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor(n_neighbors=3)
# k-최근접 이웃 회귀 모델을 훈련합니다
knr.fit(train_input, train_target)train_input, train_target으로 모델을 훈련해줍니다.
import matplotlib.pyplot as plt
# 50cm 농어의 이웃을 구합니다
distances, indexes = knr.kneighbors([[50]])
# 훈련 세트의 산점도를 그립니다
#x 축 = 길이
#y 축 = 무게
plt.scatter(train_input, train_target)
# 훈련 세트 중에서 이웃 샘플만 다시 그립니다.
plt.scatter(train_input[indexes], train_target[indexes], marker='D')
# 50cm 농어 데이터
plt.scatter(50, 1033, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
원으로 표시된 것은 존재하는 데이터, 마름모로 되어 있는 것은 삼각형이 이웃하게 되는 데이터, 삼각형은 새로 추가할 데이터입니다.
보시다시피 삼각형 데이터는 멀리 떨어져 있어서 이웃한 데이터를 찾기 곤란한 상황에 놓이게 되고, 이럴 상황이 지속될 경우 그래프가 일정 구간에서 직선이 되는 현상이 발생합니다.
# 100cm 농어의 이웃을 구합니다
distances, indexes = knr.kneighbors([[100]])
# 훈련 세트의 산점도를 그립니다
plt.scatter(train_input, train_target)
# 훈련 세트 중에서 이웃 샘플만 다시 그립니다
plt.scatter(train_input[indexes], train_target[indexes], marker='D')
# 100cm 농어 데이터
plt.scatter(100, 1033, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
극단적으로 간다면, 이런 상황에 놓이게 됩니다.
문제점 해결, 선형 회귀
from sklearn.linear_model import LinearRegression선형 회귀는 영어로 Linear Regression이라 합니다.
lr = LinearRegression()
# 선형 회귀 모델 훈련
lr.fit(train_input, train_target)선형 회귀에 train_input, train_target 데이터를 학습시킵니다.
# 훈련 세트의 산점도를 그립니다
plt.scatter(train_input, train_target)
# 15에서 50까지 1차 방정식 그래프를 그립니다
plt.plot([15, 50], [15*lr.coef_+lr.intercept_, 50*lr.coef_+lr.intercept_])
# 50cm 농어 데이터
plt.scatter(50, 1241.8, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
전보다 깔끔한 그래프가 그려졌습니다.
하지만 뭔가 아쉽습니다, 그래프가 데이터에 딱 맞게 곡선으로 되어 있다면 어떨까요?
예쁘게 곡선으로, 다항 회귀
# np.column_stack
train_poly = np.column_stack((train_input ** 2, train_input))
test_poly = np.column_stack((test_input ** 2, test_input))데이터를 제곱하여서 이차방정식을 만들 준비를 합니다.
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.predict([[50**2, 50]]))
# [1573.98423528]아까와 동일한 방식으로 학습하여 줍니다.
#기울기와 절편
print(lr.coef_, lr.intercept_)
# [ 1.01433211 -21.55792498] 116.05021078278264이차함수이므로 기울기와 절편이 존재합니다. 한번 확인해 봅시다.
# 구간별 직선을 그리기 위해 15에서 49까지 정수 배열을 만듭니다
point = np.arange(15, 50)
# 훈련 세트의 산점도를 그립니다
plt.scatter(train_input, train_target)
# 15에서 49까지 2차 방정식 그래프를 그립니다
plt.plot(point, 1.01*point**2 - 21.6*point + 116.05)
# 50cm 농어 데이터
plt.scatter([50], [1574], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
짠, 이렇게 예쁜 그래프가 완성되었습니다.
'🧠 인공지능' 카테고리의 다른 글
| 패턴 인식, 자료 분석 - SVM (0) | 2022.10.24 |
|---|---|
| FinanceDataReader로 주식 예측하기 (0) | 2022.09.21 |
| 경사하강법을 통해 오차 줄이기 (0) | 2022.09.19 |
| 기계학습에도 트리 구조가 있다? 의사 결정 트리 (0) | 2022.09.19 |
| Naive Bayes과 Iris (0) | 2022.09.04 |
